DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Théorie linéaire

DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Théorie linéaire

Il existe une théorie mathématique assez bien constituée des équations aux dérivées partielles linéaires, dont nous allons essayer de donner une idée. En contraste, les équations non linéaires présentent un foisonnement de problèmes et de méthodes dont peu sont générales. Sans que nous le précisions à chaque fois, certains des résultats que nous allons donner dans le cas linéaire se généralisent au non linéaire. Pourtant, même ceux-là font partie de la théorie linéaire, soit que la généralisation non linéaire soit limitée à des situations trop restrictives, soit qu’elle ne s’insère pas dans une théorie cohérente.

Pour pouvoir conserver les notations de la partie précédente pour les problèmes d’évolution, nous nous placerons sur un ouvert de Rⁿ⁺¹ (à l’occasion Cⁿ⁺¹ ) et nous noterons en général y = (y ⁰, y ¹,..., y ⁿ ) les coordonnées. Pour 見 捻 Nⁿ⁺¹ , nous poserons:

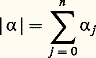
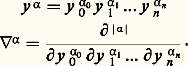Un opérateur linéaire aux dérivées partielles (on dit plus brièvement opérateur différentiel ) est défini par un polynôme à coefficients pouvant dépendre de y :

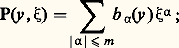il agit selon la formule:

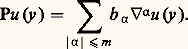m s’appelle l’ordre de P. L’opérateur P^m obtenu en ne gardant que les termes où la dérivation est d’ordre m exactement s’appelle la partie princiale de P. On notera 暴 le gradient:

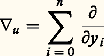(cf. CALCUL INFINITÉSIMAL - Calcul à plusieurs variables).

À côté de ces notations, il nous arrivera d’utiliser des notations en (t , x ) où t 捻 R (ou C) et x 捻 Rⁿ (ou Cⁿ ) avec des conventions analogues pour les multi-indices, puissances et dérivations.

Nous ne nous priverons pas à l’occasion de noter les distributions comme des fonctions et les produits scalaires fonctions-distributions comme des intégrales (cf. DISTRIBUTIONS).

1. Le théorème de Cauchy-Kowalewski

Supposons l’opérateur P de la forme:

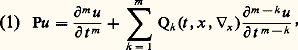où les Q^k sont des opérateurs différentiels d’ordre au plus k et où 暴^x désigne le gradient relativement à x .

Le problème de Cauchy s’énonce alors: «Trouver u vérifiant:

où f et g ⁰, g ¹,..., g ^m-1 sont des fonctions données.»

Le théorème de Cauchy-Kowalewski suppose que les coefficients de P ainsi que les données f , g ⁰, ..., g ^m-1 sont des fonctions analytiques (réelles ou complexes) de t et de x . Il affirme alors l’existence d’une solution analytique et une seule sur un voisinage de tout point (0, x ⁰). Ce voisinage dépend de P et des domaines d’analyticité complexes des données.

Ce théorème s’applique aussi aux systèmes, pourvu qu’ils soient de la forme:

où 淋 est une fonction analytique de t , x , u et ses dérivées d’ordre total m au plus mais strictement plus petit que m en t . Il reste un des rares résultats très généraux de la théorie. Il a été publié par Cauchy en 1842 dans les Comptes rendus de l’Académie des sciences .

Le travail de Sophie Kowalewski est paru en 1874; apparemment elle ne connaissait pas celui de Cauchy (et son jury non plus puisqu’il s’agissait d’une thèse!).

La démonstration d’unicité est simple et instructive. Si u est une solution analytique, elle possède un développement de Taylor en t :

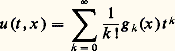où: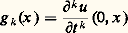

pour tout k positif cette fois. Les g ^k sont donnés pour k 麗 m . En faisant t = 0 dans l’équation aux dérivées partielles, on trouve:

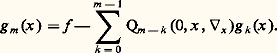En dérivant l’équation (2) par rapport à t et en y faisant t = 0, on trouve des formules analogues donnant chaque g ^k en fonction de ceux d’indices strictement plus petits.

La démonstration d’existence consiste essentiellement à démontrer la convergence de la série ainsi calculée. Elle repose sur une technique de majoration établie par Cauchy à cette occasion (méthode des séries majorantes).

La même démonstration s’applique d’ailleurs au système non linéaire (4) moyennant des complications légères.

Unicité de la solution distribution

Le théorème de Cauchy-Kowalewski n’exclut pas l’existence de solutions non analytiques au problème de Cauchy. Cette lacune a été comblée, en 1901 par le théorème de Holmgren qui affirme l’unicité des solutions «classiques» (c’est-à-dire m fois différentiables). Très élégante, la démonstration de Holmgren est remarquable pour l’époque par la façon dont elle met en jeu des idées de l’analyse moderne: dualité et densité.

Le résultat de Holmgren a été étendu par Hörmander aux solutions distributions. Il est nécessaire dans ce nouveau cadre de reformuler le problème, puisque la restriction d’une distribution à l’hyperplan t = 0, qui intervient dans les données de Cauchy, n’a a priori pas de sens. Notons la fonction qui vaut 0 pour t 麗 0 et 1 pour t 閭 0, et 嗀 la distribution de Dirac. La fonction u vérifie les conditions (2) et (3) si et seulement si on a l’équation entre distributions:

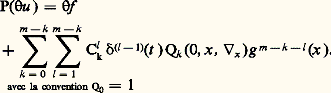En généralisant cette formule, on est amené à poser le problème de Cauchy de la façon suivante: «Trouver une distribution u à support contenu dans le demi-espace t 閭 0 qui vérifie: Pu = T, T distribution donnée à support contenu dans ce même demi-espace.»

L’unicité de la solution du problème de Cauchy devient ainsi une affirmation sur le support des distributions qui vérifient l’équation:

Si le support d’une telle distribution est contenu dans le demi-espace fermé t 閭 0, il est aussi contenu dans le demi-espace ouvert t 礪 0.

Le problème de Cauchy en coordonnées générales: hypersurfaces caractéristiques

Dans certaines situations, on a besoin d’étudier un problème de Cauchy où les données, au lieu d’être portées par l’hyperplan t = 0, le sont par une autre hypersurface . Il y a donc lieu de voir si on peut trouver des coordonnées (t , x ) telles que:

a ) l’opérateur P prend la forme (1) au produit près par une fonction non nulle (nous pourrons diviser le second membre par cette fonction); cela revient à dire que le coefficient de (face=F0019 煉^m u )/(face=F0019 煉t ^m ) ne s’annule pas;

b ) l’équation de devienne t = 0.

Supposons donc que soit définie par une équation S(y ) = 0, où S est une fonction analytique dont le gradient ne s’annule pas. Nous prenons pour nouvelles coordonnées t = S(y ) et des fonctions x ¹, ..., x ⁿ de façon que l’ensemble (t , x ) fasse un système de coordonnées. Un calcul sans histoire montre que le coefficient de (face=F0019 煉^m u )/(face=F0019 煉t ^m ) est:

Trois cas peuvent alors se présenter.

Le premier cas est dit non caractéristique: l’expression (6) est non nulle; le théorème de Cauchy-Kowalewski et celui de Holmgren s’appliquent au problème de Cauchy avec données portées par .

Le deuxième cas est le cas caractéristique, c’est-à-dire que l’équation: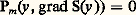

est vérifiée. On dit que est une hypersurface caractéristique . On peut démontrer dans ce cas que l’équation:

a des solutions dont le support a pour frontière, et des solutions dont les singularités sont portées par .

Il reste des cas intermédiaires où l’expression (6) s’annule, mais pas identiquement. C’est le plus délicat. Il y a lieu à ce sujet de signaler les résultats de Leray sur l’uniformisation du problème de Cauchy: la solution se ramifie autour de la variété où l’expression (6) s’annule.

Un point important à retenir est que les hypersurfaces qui peuvent faire partie de la frontière du support d’une solution de l’équation (7) sont les caractéristiques. Un autre est la caractérisation des équations elliptiques: elles n’ont pas de caractéristiques réelles. Dans le cas elliptique, il n’y a pas d’hypersurfaces pour limiter le support des solutions de (7), et pour cause: on démontre qu’elles sont analytiques.

Les limitations du théorème de Cauchy-Kowalewski ont été mises en lumière de façon particulièrement claire par Hadamard dans ses Leçons sur le problème de Cauchy (publiées à Yale en 1923 et à Paris en 1932). Elles portent sur trois points liés entre eux qui rendent le résultat inopérant dans les applications physiques:

– sa nature très locale;

– l’hypothèse d’analyticité des données; les situations physiques où l’analyticité est une propriété naturelle sont rares et en tout cas ce ne sont pas celles où se posent des problèmes de Cauchy;

– conséquence des deux circonstances précédentes, une instabilité de la solution: si on modifie les données en leur ajoutant des fonctions analytiques si petites soient elles, on perd tout contrôle de la solution, et même de son domaine d’existence, si on ne connaît pas le domaine d’analyticité complexe de la perturbation.

Ces limitations expliquent l’importance des équations hyperboliques définies comme celles où il y a encore existence pour le problème de Cauchy à données indéfiniment différentiables (ou à données distributions: si le passage de l’analytique au différentiable implique dans ce problème une différence essentielle, le passage des fonctions différentiables aux distributions est au contraire automatique pourvu que les coefficients soient eux-mêmes indéfiniment différentiables).

2. Problèmes de régularité

On a déjà signalé que si P est un opérateur elliptique à coefficients analytiques et u une distribution vérifiant l’équation (2), u est analytique sur tout ouvert où f l’est. De plus, cette propriété caractérise les opérateurs elliptiques.

On dit que l’opérateur P est hypoelliptique si toute u vérifiant (2) est indéfiniment différentiable sur tout ouvert où le second membre f est indéfiniment différentiable.

Dans sa thèse, Hörmander a donné la caractérisation suivante des opérateurs hypoelliptiques à coefficients constants:

Pour tout 見 différent de 0 on a:

La dérivée est évidemment prise par rapport à 﨡: c’est la seule variable dont dépend P puisque les coefficients sont constants. L’intervention de ces dérivées est assez naturelle du fait qu’on cherche à localiser les propriétés de u en multipliant cette distribution par une fonction indéfiniment différentiable à support borné. On utilise alors la généralisation de la formule de Leibniz, valable pour tout opérateur différentiel linéaire: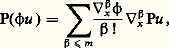

où 廓! désigne le produit des factorielles de 廓ⁱ .

Pour les opérateurs à coefficients variables (indéfiniment différentiables), on ne connaît que des conditions suffisantes d’hypoellipticité. Une de ces conditions s’exprime sur les opérateurs «à coefficients gelés», c’est-à-dire les opérateurs à coefficients constants obtenus, pour chaque point y , en remplaçant les coefficients variables b par leur valeur b (y ) désormais fixée. La condition est que chacun de ces opérateurs soit hypoelliptique et qu’ils aient tous le même domaine dans L². Une faiblesse de cette condition (obtenue à peu près simultanément par Hörmander et Malgrange) est qu’elle n’est pas conservée par les changements de coordonnées, comme le montre l’exemple de l ’équation de la chaleur.

Par la suite, Hörmander a étudié les opérateurs de la forme:

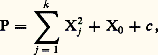où c est une fonction indéfiniment différentiable et X⁰, X¹, ..., X^k des opérateurs d’ordre un sans terme d’ordre zéro: chacun de ces opérateurs est donc défini par un champ de vecteurs (cf. équations aux DÉRIVÉES PARTIELLES - Sources et applications). Désignons par [X^j , X^l ] le commutant X^k X^l 漣 X^l X^k ; c’est encore un opérateur de la même nature et le champ de vecteurs qui lui correspond est le crochet des deux autres champs de vecteurs au sens de la géométrie différentielle. Nous noterons désormais de la même façon opérateurs du premier ordre et champs de vecteurs. Appelons encore 輻 le plus petit espace vectoriel stable par le crochet auquel X⁰, X¹, ..., X^k appartiennent et r (y ) la dimension de l’espace vectoriel formé par les valeurs au point y des champs appartenant à 輻. Cet entier r (y ) prend son maximum m sur un ouvert non vide. Si m est strictement plus petit que la dimension n + 1 de l’espace, l’opérateur P n’est pas hypoelliptique. En effet, d’après le théorème de Frobenius, on peut trouver un système de coordonnées locales dans lequel P ne contient pas de dérivations par rapport à certaines des variables. Hörmander démontre une réciproque partielle: si on a partout r (y ) = n + 1, alors P est hypoelliptique.

3. Solutions élémentaires et paramétrix

On dit qu’une distribution de deux variables E est un noyau élémentaire de P si elle vérifie la relation:

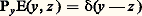qui entraîne, du moins pour f à support compact, que la distribution:

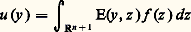vérifie l’équation (2), d’où la précision noyau élémentaire à droite qu’il est prudent d’apporter, sauf, comme nous le verrons, dans le cas des équations à coefficients constants.

Nous avons déjà rencontré un tel noyau (cf. chap. 3 L’équation de la chaleur et le type parabolique in équations aux DÉRIVÉES PARTIELLES - Sources et applications, à propos du mouvement brownien). En effet les formules (20) et (21) de cet article montrent que le noyau:

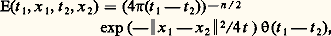où (t ) = 1 pour t positif et 0 sinon, est un noyau élémentaire pour l’opérateur de la chaleur 煉/(face=F0019 煉t ) 漣 ^x .

Le plus ancien exemple de noyau élémentaire connu est sans aucun doute celui du potentiel coulombien 漣 1/4 神 瑩y 漣 z 瑩, noyau élémentaire de l’opérateur de Laplace en dimension 3.

Opérateurs à coefficients constants et convolution

Un opérateur différentiel à coefficients constants est un opérateur de convolution puisqu’il commute avec les translations. Plus précisément:

Les noyaux élémentaires les plus commodes s’écrivent alors eux aussi comme noyaux de convolution E(y 漣 z ), où E, qui ne dépend plus que d’une variable dans Rⁿ⁺¹ , est une solution élémentaire , c’est-à-dire qu’elle vérifie: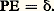

L’utilisation systématique de ce point de vue est un des traits caractéristiques du développement qu’a connu l’étude des équations aux dérivées partielles dans les années 1950 sous l’impulsion de la théorie des distributions. En particulier, Malgrange a démontré en 1953 que tout opérateur différentiel à coefficients constants non nul avait une solution élémentaire.

Solution élémentaire et hypoellipticité

Si P est un opérateur à coefficients constants hypoelliptique, ses solutions élémentaires doivent évidemment être indéfiniment différentiables en dehors de l’origine. Mais la réciproque est aussi vraie comme on va le voir. Il faut savoir que si T est une distribution indéfiniment différentiable en dehors de l’origine, alors, pour toute distribution f , le produit de convolution T f est indéfiniment différentiable sur tout ouvert où f l’est, pourvu qu’une au moins de ces deux distributions soit à support compact. Supposons donc que P ait une solution élémentaire E indéfiniment différentiable en dehors de l’origine, et soit 﨏 une fonction indéfiniment différentiable à support compact qui vaut 1 sur un voisinage de l’origine. Posons :

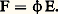Il est facile de s’assurer que:

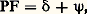où 祥 est indéfiniment différentiable à support compact. On a donc:

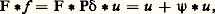la deuxième égalité à cause de l’associativité, et la commutativité du produit de convolution assurées du fait que u est le seul des trois facteurs à ne pas avoir un support compact. Comme 祥 u est indéfiniment différentiable, on voit que u est indéfiniment différentiable sur tout ouvert où f est indéfiniment différentiable.

La distribution F utilisée dans cette démonstration est ce qu’on appelle une paramétrix . Le terme n’a pas de définition mathématique précise et universellement admise. Il signifie que PF est la distribution de Dirac plus «quelque chose de pas méchant», cette dernière expression désignant en général une fonction assez régulière.

Le résultat que nous venons de donner et sa démonstration s’étendent aux opérateurs à coefficients variables moyennant des complications techniques assez sérieuses.

Solution élémentaire et hyperbolicité

On se souvient que la formulation du problème de Cauchy en théorie des distributions amène à étudier l’équation aux dérivées partielles en supposant que second membre et solution ont leur support dans le «futur» (c’est-à-dire le demi-espace t 閭 0). Si P est hyberbolique, il faut en particulier (puisque le second membre peut être la distribution de Dirac) qu’il existe une solution élémentaire dont le support est contenu dans ledit futur (dans le cas des coefficients variables, un noyau élémentaire dont le support est contenu dans l’ensemble des couples (y , z ) tels que y soit dans le futur de z ).

Inversement, supposons que l’hyperplan t = 0 soit non caractéristique et qu’il existe une solution élémentaire E à support dans le futur. Supposons aussi, mais uniquement pour simplifier, que P soit à coefficients constants. Le théorème de Holmgren assure alors que l’hyperplan t = 0 n’a que l’origine en commun avec le support de E. Il y a plus: l’intersection de ce support avec tout hyperplan t = C ^te est un compact. Il en résulte que le produit de convolution E T est défini pour toute distribution à support dans le futur. Il résout le problème de Cauchy et par conséquent P est hyperbolique.

C’est la construction de solutions élémentaires qui a permis la démonstration d’existence dans le problème de Cauchy pour les opérateurs hyperboliques du second ordre à coefficients variables, quelques dizaines d’années avant que la théorie des distributions vienne fournir le cadre général dans lequel cette méthode s’insère aujourd’hui.

Solution élémentaire et répartition asymptotique de valeurs propres

Soit A un opérateur elliptique du second ordre; pour étudier le problème de Dirichlet, restreignons-le aux fonctions qui s’annulent sur la frontière d’un ouvert borné 行; on obtient ainsi un opérateur auto-adjoint dans L²( 行) et cet opérateur est anticompact, c’est-à-dire que si un nombre n’est pas valeur propre de A, alors (A 漣I)^-1 est un opérateur compact. Supposons-le inversible pour simplifier. Un noyau élémentaire, qui résout le problème de Dirichlet, est alors donné par la formule:

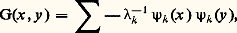où on a désigné par 漣^k les valeurs propres de A (elles sont négatives, sauf peut-être un nombre fini d’entre elles) et par 祥^k une fonction propre normée associée à^k . Un tel noyau élémentaire qui résout un problème aux limites est en général appelé noyau de Green. Supposant les^k rangées par ordre croissant, nous allons nous intéresser à leur répartition asymptotique.

Pour avoir une idée de la difficulté de ce problème, on peut considérer le cas très simple où A est le laplacien et 行 un carré de côté 1. Les^k sont alors les nombres: 神²(n ²¹ + n ²²), n ¹ et n ² entiers, ce qui nous ramène à un problème célèbre en théorie des nombres, le nombre de points de coordonnées entières contenus dans un cercle de rayon r . Notons N(r ) le nombre de valeurs de k telles que:

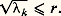Il est facile de voir que:

À la suite d’une série de travaux dont les premiers sont dus à Hermann Weyl, la partie principale de N(r ) est connue pour des problèmes elliptiques très généraux.

On se rendra compte que l’évaluation du terme en o (r ²) dans la formule (8) est un problème très difficile si on sait que, dans ce simple cas particulier, de grands efforts ont été accomplis par les théoriciens des nombres pour obtenir son ordre de grandeur et que pourtant l’exposant de r n’y est pas encore exactement connu.

Un premier outil pour aborder ce problème s’obtient en évaluant la fonction: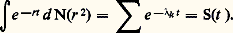

C’est la trace (somme des valeurs propres) de l’opérateur U^t associé à l’équation parabolique:

en posant:

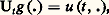où u vérifie (9) et u (0, x ) = g (x ). La trace s’obtient en intégrant le noyau de U^t sur la diagonale. Le noyau de U^t , que nous noterons U(t , x , y ) s’écrit:

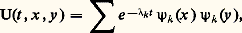de sorte que:

Dans un travail paru en 1973, Colin de Verdière a mis ces idées en œuvre dans un contexte légèrement différent: A est l’opérateur de Laplace-Beltrami sur une variété riemannienne compacte X. Une construction par approximations successives de U lui permet de montrer que l’existence de géodésiques fermées et leur longueur influent sur le comportement asymptotique des valeurs propres.

Immédiatement après, Chazarain, d’une part, et Duistermat et Guillemin, d’autre part, ont obtenu des résultats analogues par une méthode légèrement différente dans laquelle la cause de l’intervention des géodésiques fermées est plus apparente. Elle s’obtient en complétant N par antisymétrie (N(face=F0019 漣 r ) = 漣 N(r )) et en prenant la transformée de Fourier de sa dérivée: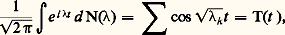

équation purement symbolique entre distributions. La distribution T ainsi obtenue est associée à l’opérateur hyperbolique:

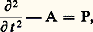comme la fonction S l’était à un opérateur parabolique. En effet, si on définit l’opérateur V^t en posant:

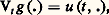où u est la solution du problème de Cauchy:

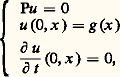on trouve que T est la «trace-distribution» de V^t . En fait, V^t n’est pas un opérateur à trace, mais, pour 﨏 indéfiniment dérivable à support compact,

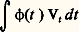en est un et sa trace n’est autre que:

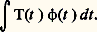On remarquera que V^t s’obtient à partir d’une solution élémentaire de P en dérivant par rapport à t .

Si on se rappelle ce qui a été expliqué (cf. chap. 1 L’équation des ondes et le type hyperbolique in équations aux DÉRIVÉES PARTIELLES - Sources et applications, au sujet des bicaractéristiques), on ne s’étonnera pas des deux résultats suivants:

– les bicaractéristiques de P s’obtiennent en parcourant à une vitesse unité les géodésiques de X;

– les singularités de V^t se propagent selon ces bicaractéristiques.

En particulier, si X possède une géodésique fermée de longueur L, on va voir revenir une singularité dans V^t avec une période L. Ce type de résultats a été étendu par la suite, en particulier au problème de Dirichlet. Le rôle des géodésiques fermées est alors joué par les lignes polygonales qui se referment par réflexion sur la frontière. On en déduit (pas directement!) que les singularités de T sont des points de la forme k L. Ce qui se traduit enfin sur le comportement asymptotique de N en vertu d’un des aspects de la dualité régularité locale-décroissance à l’infini dans la transformation de Fourier.

4. La transformation de Fourier et ses généralisations

Nous emploierons les notations suivantes pour la transformation de Fourier:

où n est la dimension de l’espace (cf. DISTRIBUTIONS, chap. 4, et analyse HARMONIQUE, chap. 3).

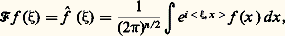Il en résulte que:

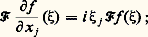en d’autres termes, la transformation de Fourier transforme la dérivation partielle en produit par la variable correspondante, au facteur i près. Si P est un opérateur différentiel à coefficients constants et u et f des distributions tempérées, l’équation aux dérivées partielles (2) équivaut à:

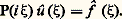Nous utiliserons le fait que la transformation de Fourier est inversible et a pour inverse 杻 définie par:

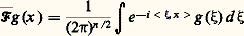et le théorème de Parseval, étroitement lié au résultat précédent: 杻 est une isométrie de L²(Rⁿ ).

Une conséquence simple de ces résultats est que la transformation de Fourier et son inverse ont exactement les mêmes propriétés.

La dualité régularité locale-décroissance à l’infini

La transformée de Fourier d’une fonction intégrable est bornée. Si une fonction a des dérivées intégrables, sa transformée de Fourier décroît donc comme 1/ 瑩 﨡 瑩, et si elle a des dérivées d’ordre k intégrables sa transformée de Fourier décroît à l’infini en 瑩 﨡 瑩^-k . Inversement, si la transformée de Fourier û de u décroît à l’infini comme 瑩 﨡 瑩^-k , u a des dérivées jusqu’à l’ordre k 漣 n 漣 1 qui sont continues et bornées.

Le décalage disparaît, grâce au théorème de Parseval, si on considère les fonctions de carré intégrable. Ainsi u appartient à l’espace de Sobolev H¹(Rⁿ ) (cf. chap. 2 Le type elliptique in équations aux DÉRIVÉES PARTIELLES - Sources et applications) si et seulement si sa transformée de Fourier est de carré intégrable pour la mesure (1 + 瑩 﨡 瑩²) d 﨡. Ce résultat fournit la définition la plus simple de l’espace de Sobolev d’indice réel quelconque: une fonction appartient à l’espace H^s (Rⁿ ) si sa transformée de Fourier est de carré intégrable pour la mesure (1 + 瑩 﨡 瑩²)^s d 﨡. L’introduction d’indices non entiers est nécessaire surtout du fait que, pour s 礪 1/2, on sait définir la restriction à un hyperplan d’une fonction appartenant à H^s , et cette restriction appartient à H^s 漣1/2; de plus, toute fonction appartenant à H^s size=1^漣1/2 de l’hyperplan est restriction d’une fonction appartenant à H^s de l’espace ambiant.

Un cas extrême de décroissance à l’infini est donné par un support compact. Il lui correspond du côté Fourier une propriété d’analyticité: une distribution est à support compact si et seulement si sa transformée de Fourier se prolonge en une fonction analytique sur Cⁿ tout entier à croissance exponentielle à l’infini (théorème de Paley Wiener généralisé). Il est bon de remarquer ici que la croissance exponentielle à l’infini de l’extension à Cⁿ apparaît en même temps comme une propriété locale de la fonction puisqu’on peut la caractériser sur la suite des dérivées en un point via le développement de Taylor.

Propriétés des solutions élémentaires

Tout polynôme non nul possède un inverse multiplicatif qui est une distribution tempérée. Par transformation de Fourier, cela revient à dire que tout opérateur différentiel à coefficients constants possède une solution élémentaire tempérée.

Voyons d’abord comment ce résultat permet de démontrer l’hypoellipticité des opérateurs elliptiques. Soit P un tel opérateur. L’ellipticité signifie que la partie principale P^m ( 﨡) n’a pas de zéro réel non nul et, par homogénéité, il en est de même de P^m (i 﨡). Soit E une solution élémentaire tempérée. On a pour tout 見:

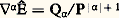où Q size=1^見 est un polynôme de degré | 見| (m 漣 1). Par conséquent, 暴 size=1^見Ê décroît à l’infini comme 1/ 瑩 﨡 瑩^m+ | size=1^見|. En particulier, ^k Ê décroît comme 瑩 﨡 瑩^-(m+2k) , ce qui montre, en revenant «côté x », que 瑩x 瑩^2k E est m + 2k 漣 n 漣 1 fois continûment dérivable et, par division, que E est m + 2k 漣 n 漣 1 fois dérivable en dehors de l’origine. Mais k peut être choisi aussi grand qu’on veut, d’où l’indéfinie différentiabilité de E en dehors de l’origine.

Ce raisonnement s’adapte d’ailleurs au cas général des opérateurs hypoelliptiques à coefficients constants, à condition de savoir que, si P( 暴) est hypoelliptique, P(i 﨡) croît à l’infini comme une puissance strictement positive de 瑩 﨡 瑩. Cette propriété se démontre grâce à une combinaison du développement de Puiseux et du théorème de Tarski-Seidenberg (l’image par une application polynomiale d’un ensemble défini par des équations et inéquations polynomiales est un ensemble de même nature).

Passons aux opérateurs hyperboliques. Il s’agit ici de savoir s’il y a une solution élémentaire dont le support est contenu dans le demi-espace t 閭 0 et qui coupe tout hyperplan t = C ^te selon un compact. Le résultat essentiel est une généralisation du théorème de Paley Wiener, le théorème de Plancherel. Sous sa forme la plus simple, il dit qu’une distribution tempérée d’une variable est à support contenu dans la demi-droite x 閭 a si et seulement si sa transformée de Fourier est limite, pour 兀 tendant vers 0, d’une fonction F analytique dans le demi-plan complexe 兀 礪 0 qui vérifie une inégalité :

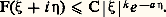À plusieurs variables, le théorème exprime une dualité entre distributions à support dans un convexe et fonctions analytiques sur Rⁿ +i 臨 vérifiant une condition de croissance, où 臨 est un cône convexe.

On conçoit donc que P sera hyperbolique si P(i 精, i 﨡) est non nul sur un ensemble Rⁿ⁺¹ + i 臨. Toutefois, sous cette forme, la condition n’est pas nécessaire parce que la solution élémentaire à support dans le futur peut ne pas être tempérée. Une condition nécessaire et suffisante d’hyperbolicité est que l’hyperplan t = 0 soit non caractéristique et qu’il existe 精⁰ tel que:

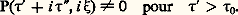Mais cette condition est équivalente à la condition apparemment plus forte: il existe 精⁰ et un cône convexe ouvert 臨 tels que:

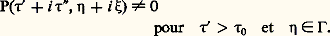Une condition nécessaire plus simple est que, pour tout 﨡 réel, le polynôme en 精 P^m ( 精, 﨡) ait toutes ses racines réelles; une condition suffisante est que de plus ces racines soient simples pour 﨡 0. Ces conditions portant sur la partie principale se généralisent aux opérateurs à coefficients variables.

Opérateurs pseudo-différentiels et opérateurs intégraux de Fourier

On voit qu’on dispose d’outils puissants pour l’étude des équations aux dérivées partielles à coefficients constants. Le passage aux coefficients variables a souvent consisté à se ramener aux coefficients constants. L’idée est que, les coefficients étant continus, localement l’équation est assez proche d’une équation à coefficients constants, ce qui permet soit des majorations, soit des approximations successives.

À partir des années 1960, on a développé des outils permettant de travailler plus systématiquement sur les équations à coefficients variables. Grâce aux propriétés de la transformation de Fourier, on peut écrire:

On généralise cette formule en n’y supposant plus que P soit un polynôme en 﨡. On dit qu’on a affaire à un opérateur pseudo-différentiel d’ordre m s’il vérifie les inégalités: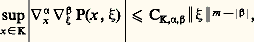

pour tout compact K et tout 﨡 différent de 0. Le cas effectivement utilisé est celui où P est somme d’une fonction positivement homogène de degré m en 﨡 et d’un deuxième opérateur pseudo-différentiel d’ordre strictement plus petit que m .

Les opérateurs pseudo-différentiels permettent de plonger les opérateurs différentiels dans une algèbre où se trouvent aussi leurs paramétrix. Ils jouent ainsi le rôle qui est pour les opérateurs à coefficients constants, celui de la convolution. Ce cadre est très bien adapté au calcul de paramétrix, du moins dans le cas elliptique. Dans les autres cas, on en tire parti en passant au point de vue microlocal (cf. équations aux DÉRIVÉES PARTIELLES - Analyse microlocale).

L’étape suivante est le passage aux opérateurs intégraux de Fourier . La généralisation consiste à remplacer dans la formule (10) la phase 麗 﨡, x 漣 y 礪 par une fonction plus générale.

Un cas particulier de cette méthode avait été employé par les physiciens en optique ondulatoire, c’est le développement en ondes sphériques. Pour une onde monochromatique:

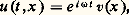l’équation des ondes devient l’équation de Helmholtz:

où k = 諸/c . Cette équation admet la solution élémentaire:

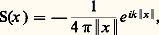d’où des solutions de la forme: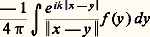

(il s’agit soit de l’équation avec second membre correspondante, soit plus souvent de fonctions qui vérifient (11) en dehors du support de f ). Une intégration par rapport à k permet de passer à d’autres solutions de l’équation des ondes.

Encyclopédie Universelle. 2012.